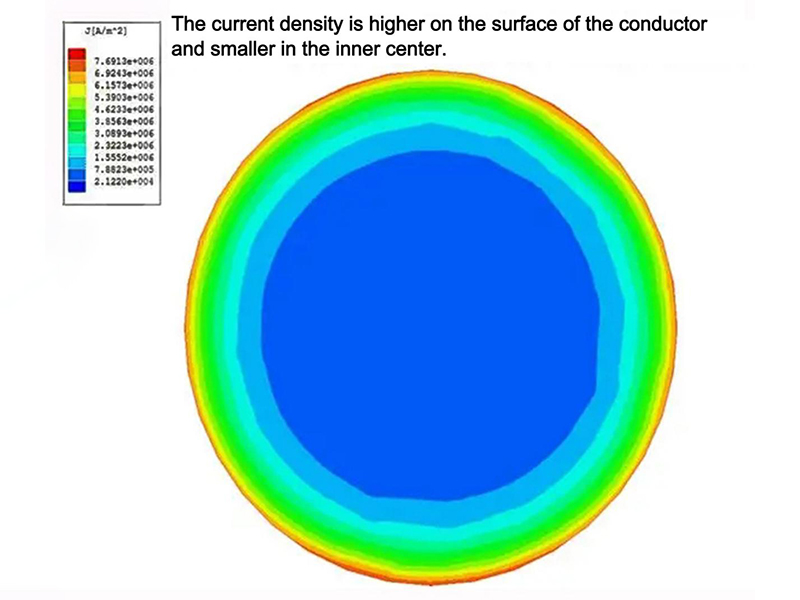
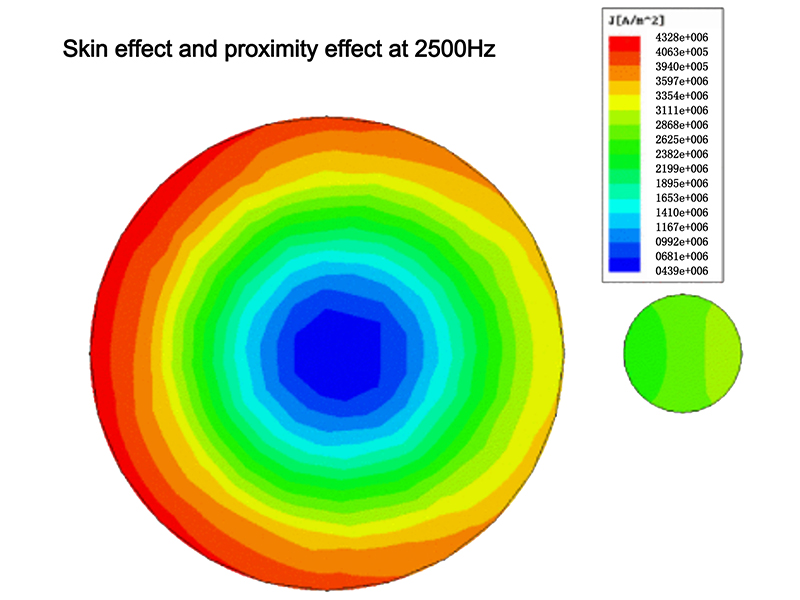
When there is alternating current or alternating electromagnetic field in the conductor, the current distribution inside the conductor is uneven. The current is concentrated in the “skin” part of the conductor, that is, the current is concentrated in the thin layer on the surface of the conductor. The closer the current is to the surface of the conductor, the greater the current density, and the actual current inside the conductor is smaller. As a result, the resistance of the conductor increases, so does its loss power. This phenomenon is called skin effect.
Skin effect
When calculating the resistance and inductance of a wire, it is assumed that the current is uniformly distributed on its cross section. Strictly speaking, this assumption is only true when the current change rate (di/dt) in the conductor is zero. Another way is to ensure that the current density is uniform when the conductor passes through DC. Or if the current change rate is very small, the current distribution can still be considered as uniform. This statement is still reliable for thin wires operating at low frequencies.
However, in high-frequency circuits, the current rate of change is very large, and the uneven distribution is very serious. The magnetic field generated by high-frequency current in the wire induces the maximum electromotive force in the central area of the wire. Because the induced electromotive force generates induced current in the closed circuit, the induced current in the center of the conductor is the largest. Because the induced current is always in the direction of reducing the original current, it forces the current to be limited to the place near the outer surface of the wire. The effect is mainly caused by the eddy electric field generated in the conductor by the changing electromagnetic field, which counteracts the original current.
The effect that the alternating current in a conductor increases the current density near the conductor surface. On the cross section of a straight long conductor, the constant current is uniformly distributed. For alternating current, self induced electromotive force appears in the conductor to resist the passage of current. The magnitude of this electromotive force is proportional to the magnetic flux cut by the conductor per unit time. Take the conductor of circular cross-section as an example, the closer to the conductor center, the greater the self induced electromotive force generated by the external magnetic field line; The closer to the surface, the less affected by the growth and decline of its internal magnetic field lines, so the self induced electromotive force is small. This leads to a higher current density near the conductor surface. Since the self induced electromotive force increases with the increase of frequency, the skin effect becomes more significant with the increase of frequency. Skin effect reduces the effective sectional area of the conductor when it passes through the current, thus increasing its effective resistance.
The skin effect can also be explained by the process of electromagnetic wave penetrating into the conductor. When the electromagnetic wave penetrates into the conductor, it gradually attenuates due to energy loss. When the wave amplitude attenuates to 1/E times of the surface wave amplitude, it is called the penetration depth of the alternating electromagnetic field to the conductor. Taking the penetration of plane electromagnetic wave into a semi infinite conductor as an example, the penetration depth is in the equation ω Is the angular frequency, γ Is the conductivity of the conductor, μ Is the permeability. It can be seen that the penetration depth is inversely proportional to these three quantities. The wavelength of the electromagnetic wave in the conductor is 2z0. Whether the skin effect is significant can also be judged by comparing the conductor size with the electromagnetic wave length. If the thickness of the conductor is larger than this wave in the conductor, the skin effect will be significant.
Post time: Nov-25-2022